[翻译]一种PLNN的精确一致解释:封闭解析法

Posted on

by WiiGe

读了一篇论文 KDD 2018 的长报告论文，《Exact and Consistent Interpretation for Piecewise Linear Neural Networks: A Closed Form Solution》，讲的是如何明确解释分段线性神经网络(PLNN)的整体行为。

几位Simon Fraser University的作者通过证明PLNN严格等价于一组局部线性分类器(LLCs)，以简洁的解析形式给出了一种准确、一致的神经网络解释方法——OpenBox，还很高效。文内的实验结果表明，OpenBox 不仅可以准确、一致地描述PLNN的总体行为，还能够对PLNN进行有效的调试和排错。

啥是PLNN？为什么要解释它？

分段线性神经网络(PLNN) 是一种采用了如MaxOut和ReLU函数族的分段线性激活函数的神经网络，其激活函数在不同的定义域区间内对应不同的线性函数。对于这样的神经网络，我们有必要解释每次独立预测背后的基本原理，这样才能使我们更容易信任/不信任预测结果, 让我们更坚定自如地应用其判断。

  • 我们想知道: 为什么一个模型做出这样的预测?复杂的神经网络模型都像黑箱一样,无法去感知它的内部工作状态
  • 如果一个解释是不准确的，我们就无法确定解释结果和模型的真实决策是否相符，解释本身就是不可信的
  • 如果对于多个相似实例的解释不一致，我们将不可避免地遇到多个解释自相矛盾的情况，解释的有效性也会因此受到质疑

已有工作

对于神经网络的解释，现存的大概有以下三种方法：

  • 隐神经元分析法 ：通过可视化，恢复映射或者标记隐层神经元学习到的特征来解释预训练的神经网络。定性分析每个神经元很难为整个神经网络的全局机制给出多少定量的解释。
  • 模仿者模型法：构建了一个易于解释并有着很高分类精度的透明模型。模仿模型的解释与目标深度神经网络的实际整体机制之间总是存在差距。
  • 局部解释法：通过分析其局部扰动的预测值来计算和可视化输入实例的重要特征。但是对从某些角度无法区分的实例的解释可能会不一致。

如何解释PLNN? OpenBox

文章提出了一种全新的方法叫做OpenBox，这一方法通过数学证明其解析式的存在且可解证明了OpenBox的决策行为与原PLNN完全精确且一致。文章给出了对PLNN等价模型的精确性和一致性的定义：

  • 准确性：M数学上等价于N，由M得出的解释能原本地描述N的确切行为
  • 一致性：M能为相似实例分类给出相似的解读/解释

得出OpenBox这一模型的思路其实并不复杂：如果你需要解释一个PLNN，最好的方式就是得出其等价的数学解析式。文章在这里用到了一个PLNN的特性，即PLNN一定是分段线性函数，所以对同一个神经元来说，一个固定输入只会触发整个激活函数中的那一段。 将所有隐层神经元的激活状态按下图所示的绿色虚线顺序排列成一个向量 Conf(x)。这个向量被称作 PLNN 对输入实例 x 的状态(Configuration)。

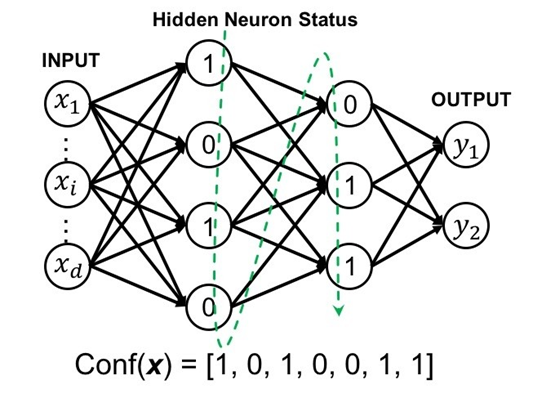
如果PLNN 的网络结构和参数都给定，那么所有神经元的激活状态都唯一依赖于输入实例 x，因此 Conf(x) 由输入实例 x 唯一决定。因为 x 本身是一个给定常量，所以 Conf(x) 也是一个常量。因此，图中 PLNN 的每个隐层神经元的运算实质上都是由常量 Conf(x) 所确定的线性运算。

对于任意给定的输入实例 x，整个 PLNN 严格等价于\(F(x)=softmax(\hat{W}^{(1:L-1)}*x+\hat{b}^{(1:L-1)})\)这一线性分类器，其中W是全部神经元的权重，b是每个神经元的偏置，L是所有隐层的层数。输出层采用softmax函数，那么可知这个F(x)即是等价PLNN的决策面。

每一个隐层神经元的输入 z 都必须满足由该神经元激活状态所决定的线性不等式约束。每个隐层神经元的输入 z 都是输入实例 x 的线性函数，所以这组关于输入 z 的线性不等式约束实质上是对输入实例 x 的一组线性不等式约束。

若令这些约束的集合为P，显然，所有满足 P 中线性不等式约束的输入实例 x 都具有相同的 Conf(x)，因此这些实例共享相同的线性分类器(LLC)并具有完全一致的解释。P 中的每一个不等式都定义了一个线性边界，所有线性边界一起组成了一个凸包(Convex Polytope，CP)，凸包中的所有输入实例都满足 P 中的所有不等式。

因此这些输入实例 x 都具有相同的 Conf(x)且共享同一个线性分类器。这个存在于局部区域的凸包和它所对应的线性分类器统称为局部线性分类器(Local Linear Classifier，LLC)。对于任意给定的 PLNN，不同的隐层神经元激活状态对应着不同的 Conf(x)，而每一个 Conf(x) 都确定了一个LLC。因此，一个 PLNN 严格等价于一组LLC。我们把这组LLC的集合标记为 M，而M 就是 PLNN 的等价解释模型。

OpenBox算法

OpenBox的算法流程如下：

算法 1: OpenBox (?,?_?????)
输入：?:= 恒定PLNN，?_?????∈χ为用于训练?的训练实例
输出：ℳ:= 一个活动LLCs的集合
  初始化：ℳ= ∅, ?=∅
   for each ? ∈ ?_????? do
    通过?_ℎ←????(?)计算状态数
    if ?_ℎ ∉ ? then
      ? ← ?∪?_ℎ且ℳ←ℳ∪(?_ℎ (?) ,?_ℎ )
    end if
   end for
   return ℳ

文章翻译&原文下载

最后把下载放这儿吧：

  • 试着翻译的论文可以在这里下载
  • 几篇本文相关的前置工作存档在这里
  • 原文保存在这里 ，原文如果无法访问，在这里能找到我这的存档

Published by

WiiGe