该系列是C++的一个总结, 以便复习和记忆
我们都知道,类型决定了数据所占的比特数以及如何解释这些比特的内容, 占用的比特数限制了该类型能表示的数据范围.
计算机里可寻址的最小内存块是字节(Byte), 不过字(Word)才是存储的基本单元, DWord和QWord就是所谓的双字和四字了
在C++中一个char和一个机器字节长度一样，一般都是8-bit
C++的算数类型如下:
| 类型 | 含义 | 最小大小 |
|---|---|---|
| bool | 布尔型 | - |
| char | 字符 | 8 bit |
| wchar_t | 宽字符 | 16 bit |
| char16_t | Unicode字符 | 16 bit |
| char32_t | Unicode字符 | 32 bit |
| short | 短整型 | 16 bit |
| int | 整型 | 16 bit |
| long | 长整型 | 32 bit |
| long long | 长整型 | 64 bit |
| float | 单精度浮点数 | 6位有效数字 |
| double | 双精度浮点数 | 10位有效数字 |
| long double | 扩展双精度浮点数 | 10位有效数字 |
C++中的字面值(literal)是一种可以望文得义的直观常量, 对于char类型而言, 单引号’ ‘括起来的一个字符是char型的字面值, 而双引号” “括起来的字符(包括0个)都是字符串(string), 字符串以”\0″结尾, 因此其长度比它看上去(实际内容)要大1.
如果要在代码中显式指定字面值类型, 那么可以看看这一个表:
| 字符和字符串字面值 | |||
| 前缀 | 类型 | 含义 | 示例 |
| u | char16_t | Unicode16字符 | u'M' |
| U | char32_t | Unicode32字符 | U'M' |
| L | wchar_t | 宽字符 | L'M' |
| u8 | char | UTF-8(字符串Only) | u8"HelloWorld!" |
| 整型字面值 | 浮点型字面值 | ||
| 后缀 | 类型 | 后缀 | 类型 |
| u or U | insigned | f or F | float |
| l or L | long | l or L | long double |
| ll or LL | long long | ||
对于基本类型的存储有一个可以展开的论题:大小端存储和数的表示
大小端存储
大小端存储的理解并不困难:
按照最高有效字节到最低有效字节的顺序存储对象, 尾端存放在高地址处 ==> 大端(Big-Endian), 即高尾端存储
表现为地址由小向大增加，而数据从低位往高位放
按照最低有效字节到最高有效字节的顺序存储对象, 尾端存放在低地址处 ==> 小端(Little-Endian), 即低尾端存储
表现为地址由小向大增加，而数据从高位往低位放
大端&小端的提法源于多个字节值的哪一端存储在该值的起始地址: 小端是低位存储高序字节, 大端是低位存储高序字节. 因此大小端也被称为机器数存储的字节序
最高有效位(most significant bit, MSB)是一个32位值最左边1位，最低有效位(least significant bit, LSB)是一个32位值最右边1位
对于一个16进制32位数0x12345678, 可以得到这样的表格
| 第1个字节 | 第2个字节 | 第3个字节 | 第4个字节 | |
|---|---|---|---|---|
| 32位值原值 | 最高有效位(MSB) | ---- ---- | ---- ---- | 最低有效位(LSB) |
| 0x12345678按位表示的真值 | 0001 0010(0x12) | 0011 0100(0x34) | 0101 0110(0x56) | 0111 1000(0x78) |
| 内存地址 | 低地址 | ---- ---- | ---- ---- | 高地址 |
| 大端存储 | 0x12 | 0x34 | 0x56 | 0x78 |
| 小端存储 | 0x78 | 0x56 | 0x34 | 0x12 |
用Code::Blocks写一段C++来验证一下:
#include <iostream>
using namespace std;
int main()
{
unsigned int d1=0x12345678;
int d2=0x12345678;
unsigned int d3=0x123456789abcdef;
unsigned int d4=0x123456789abcdeffff;
cout << "Wait! It's Printing" << endl;
return 0;
}
点开Debug菜单里面的DebuggingWindows调出MemoryDump, 我们可以看看这台PC上如何存储这个值:
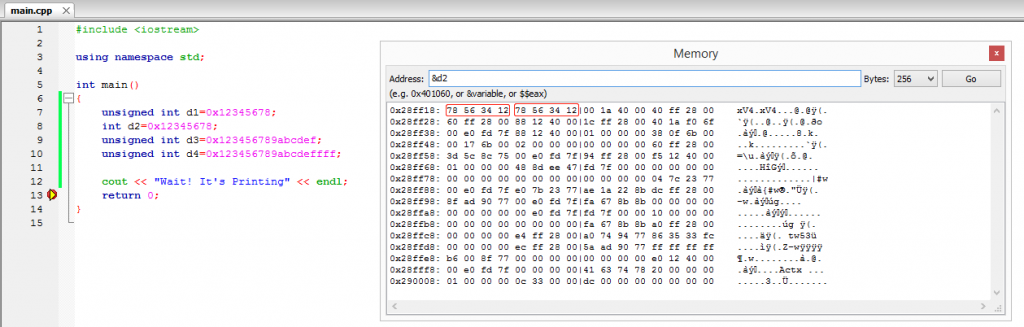
上图两个标注出来的红框里, 左框是变量d2, 右框是d1.
显而易见, 在这个内存地址从左至右递增的视图上, 我们看到低位内存地址上存储着该32位值的高位字节0x78，而高位地址(左数第4个字节)上存储着该值的低位字节0x12
——这是明显是小端存储
而且这一事实说明了, 数据类型决定了数据所占的比特数以及如何解释这些比特的内容, 无论是unsigned int还是int, 其二进制真值都是相同的
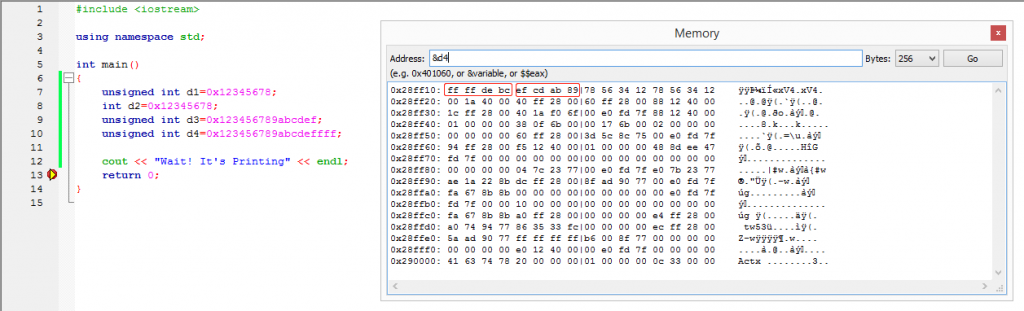
这张图里的两个红框指的是d4和d3, 在代码中我们为其赋予了超过32位的值: 0x123456789abcdef 和 0x123456789abcdeffff
按照小端存储, 这两个值的存储顺序应该为0xef 0xcd 0xba 0x89 0x67 0x45 0x32 0x01和0xff 0xff 0xde 0xbc 0x9a 0x78 0x56 0x34 0x21
但是int和unsigned int只能储存32bit二进制值, 因此存储了高位舍弃了低位(似乎是为了减少精度损失, 和浮点数的理念相似), 变成了0xef 0xcd 0xba 0x89和0xff 0xff 0xde 0xbc
这时我们不得不实际去谈一谈计算机中的数的表示了
数的表示
计算机中数的表示是个内容不少的论题, 这里只讨论整数的情况, 浮点数相关我打算单独总结成文
先说说一个数的机器数,机器数即一个数在计算机里的二进制下表示, 而将带符号位的机器数对应的真正数值称为机器数的真值
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值.
反码的表示方法是：正数的反码 = 其本身, 负数的反码是在其原码的基础上, 符号位不变，其余位按位取反.
补码的表示方法是：正数的补码 = 其本身, 负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即反码+1)
贴一张老图来说明各种表示法之间转换的计算方式:
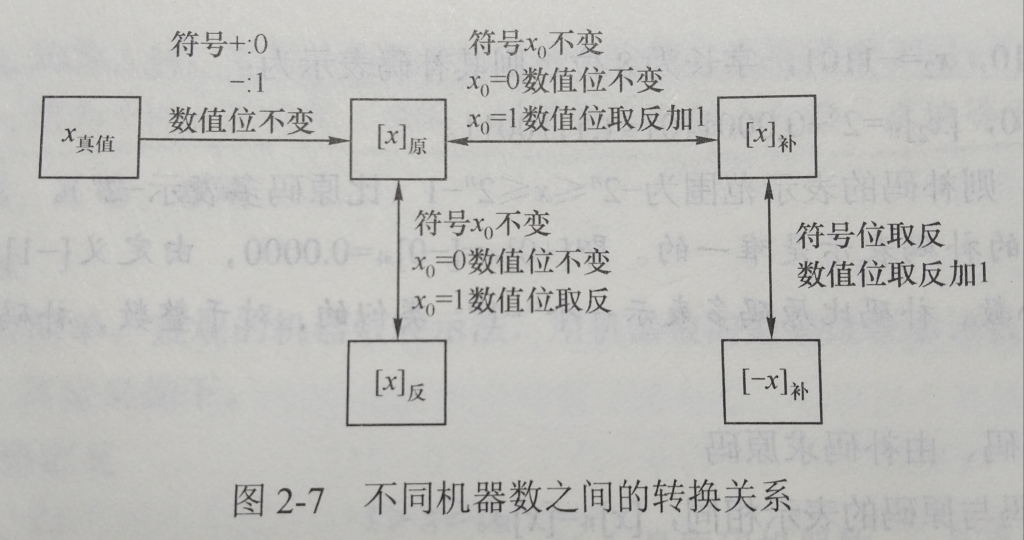
现在我们实际考虑一下整数的表示方法, 显然32位无符号整数的情况最为简单. 只有32个0和1的序列, 没有符号. 我们很容易想到————最大值就是全1而最小值是32位全0
最小值\(0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ =\ 0\)
最大值\(1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ 4294967295 = 2^{32}\ -\ 1\)
这是无符号的32位整数能表示的最大值
这很直观, 现在来我们来看看不怎么直观的——有符号的int
int用最高位作为符号位，0表示正数, 1表示负数, 于是只有31位能表示绝对值
显然, 最大值只能是\(0111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ 2147483467= 2^{31}\ -\ 1\)
那么, 最小值是多少呢?如下表
| 真值 | 原码 | 原码(十六进制) | 补码(二进制) | 补码(十六进制) |
|---|---|---|---|---|
| 2147483467 | 0111 1111 1111 1111 1111 1111 1111 1111 | 0x 7F FF FF FF | 0111 1111 1111 1111 1111 1111 1111 1111 | 0x 7F FF FF FF |
| 1 | 0000 0000 0000 0000 0000 0000 0000 0001 | 0x 00 00 00 01 | 0000 0000 0000 0000 0000 0000 0000 0001 | 0x 00 00 00 01 |
| 0 | 0000 0000 0000 0000 0000 0000 0000 0000 | 0x 00 00 00 00 | 0000 0000 0000 0000 0000 0000 0000 0000 | 0x 00 00 00 00 |
| -0 | 1000 0000 0000 0000 0000 0000 0000 0000 | 0x 80 00 00 00 | 0000 0000 0000 0000 0000 0000 0000 0000 | 0x 00 00 00 00 |
| -1 | 1000 0000 0000 0000 0000 0000 0000 0001 | 0x 80 00 00 01 | 1111 1111 1111 1111 1111 1111 1111 1111 | 0x FF FF FF FF |
| -2 | 1000 0000 0000 0000 0000 0000 0000 0010 | 0x 80 00 00 02 | 1111 1111 1111 1111 1111 1111 1111 1110 | 0x FF FF FF FE |
| -129 | 1000 0000 0000 0000 0000 0000 1000 0001 | 0x 80 00 00 82 | 1111 1111 1111 1111 1111 1111 0111 1111 | 0x FF FF FF 7F |
| -2147483648 | 32bit无法表示 | 32bit无法表示 | 1000 0000 0000 0000 0000 0000 0000 0000 | 0x 80 00 00 00 |
因此我们能够得到一个比较直观的, 按二进制递增的32位int补码对照表:
| 补码(二进制) | 真值 | 补码(十六进制) |
|---|---|---|
| 0000 0000 0000 0000 0000 0000 0000 0000 | 0 | 0x 00 00 00 00 |
| 0000 0000 0000 0000 0000 0000 0000 0001 | 1 | 0x 00 00 00 01 |
| 0000 0000 0000 0000 0000 0000 0000 0010 | 2 | 0x 00 00 00 02 |
| ...... | ...... | ...... |
| 0111 1111 1111 1111 1111 1111 1111 1110 | 2147483466 | 0x 7F FF FF FE |
| 0111 1111 1111 1111 1111 1111 1111 1111 | 2147483467 | 0x 7F FF FF FF |
| 1000 0000 0000 0000 0000 0000 0000 0000 | -2147483648 | 0x 80 00 00 00 |
| 1000 0000 0000 0000 0000 0000 0000 0001 | -2147483647 | 0x 80 00 00 01 |
| 1000 0000 0000 0000 0000 0000 0000 0010 | -2147483646 | 0x 80 00 00 02 |
| ...... | ...... | ...... |
| 1111 1111 1111 1111 1111 1111 1111 1110 | -2 | 0x FF FF FF FE |
| 1111 1111 1111 1111 1111 1111 1111 1111 | -1 | 0x FF FF FF FF |
这时我们就很好理解书中所讲这一概念:
化减为加是补码表示的一个方面, 我们可以理解为符号位把这\(4294967296 = 2^{32}\)种表示方式分成了两半,然后用多出来的一个负数0表示多出来的那个-2147483648, 实际上是实现了从[-2147483648, 2147483647]到[0, 4294967295]的一种映射
映射背后的机制
用映射来理解补码其实也并不是很直观, 虽然正数部分完全没问题: 随着最大值0的增大, 补码的二进制表示值\(0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\)也是递增的
不过负数部分就不是这样了, 最大值\(0111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ 2147483467\)之后加1会直接跳到最小值\(-2147483648\), 然后再随着补码的二进制表示值增大而真值递增到\(1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ -1\)
对于这个反直觉的跳变, 有一个不错的理解思路——同余
求余数是一个数学上的概念, 而求模(模除)则是一个计算机科学的概念
(顺便背个单词:被除数是dividend, 除数是divisor, 商是quotient, 余数则是remainder)
模除(Modulo)这一运算,维基百科给了这么个定义:
当 \(a\ =\ bq\ +\ r\),\(q\)是整数, 并使其最大, 此时我们说\(a\)模除\(b\)等于\(r\), 记作\(a\ mod\ b\ =\ r\)
有
$$a\ mod\ b\ =\ a-\ b\ *\ \left\lfloor\frac{a}{b}\right\rfloor $$
而数学上的余数(Remainder)在维基百科的定义是这样的:
若\(a\)和\(d\)是两个自然数，\(d \neq 0\)，可以证明存在两个唯一的整数\(q\)和\(r\)，满足\(a\ =\ dq\ +\ r\)且\(0 \le r \lt d\), \(q\)被称为商, \(r\)被称为余数
显然在浮点数时这个定义就毫无意义了, 除非限定商为一个整数, 不过————负整数呢?
我们可以轻松找到一个负数的多个满足\(a\ =\ bq\ +\ r\)的余数, 比如 \((-36)\ =\ 13*(-3)\ +\ 3\)和\((-36)\ =\ 13*(-2)\ +\ (-10)\)
我把这两个余数称为正余数\(pr\)和负余数\(nr\), 对于被除数\(d\)显然有\(pr = d + nr\)
于是,有人写了这样一篇博文来探究不同语言是如何取舍正负余数的. 其实实现求余主要就两种方法:截断(truncate)和取整(floor)
截断的思路很简单:舍去小数
$$r\ =\ a\ -b* turncate(\frac{a}{b})$$
取整听说是大佬Donald Knuth提出的, 想法也很简单: 向下取整
$$r\ =\ a\ -b* \left\lfloor\frac{a}{b}\right\rfloor$$
以上例\((-36)\ mod\ 13\)来说截断法会得出\((-10)\), 而取整法则会得出\(3\)
所以在那篇博文中, 博主试了几种语言之后发现有的语言尽量让商大一些而一些语言试图让商小一些, 其实他们只是用了不同的模除实现方式罢了吧
我也在Code::Blocks里随手写了几行丑陋的代码来枚举两种余数:
#include <iostream>
#include <string>
using namespace std;
void RaeainedCalculator(long a,long b)
{
string tempResult = to_string(a) + " % " + to_string(b) + " = ";
long r1 = a % b;
long r2 = 0;
if(r1 == 0)
{
tempResult += r1;
return;
}
else
{
if(r1 > 0)
{
r2 = r1- b;
}
else
{
r2 = r1 + b;
}
tempResult += (to_string(r1) + " & " + to_string(r2));
}
cout<< tempResult<<endl;
}
int main()
{
long divisor =0 , dividend =0,quotient = 0, remainder = 0;
do
{
cout<<"输入0退出"<<endl;
cout<<"请输入除数与被除数:"<<endl;
cin>>divisor>>dividend;
if(divisor>0 && dividend>0)
{
cout<<to_string(divisor) + " % " + to_string(dividend) + " = " + to_string(divisor%dividend)<<endl;
}
else{
RaeainedCalculator(divisor,dividend);
}
}
while(divisor != 0);
return 0;
}
那么现在让我们回到32位int——虽然其能表示的所有可能值是\(4294967295 = 2^{32}\)个,但被正负分成两部分之后, 只有31位能够按权展开, 那么最大值只能是\(2147483647\),
所以要找到一个负数在32位表示法中的同余数只需要用正负余数去反推这个另一个数就行了.
比如\((-100)\ mod\ 2147483647\ =\ (-100)\), 可推知其正余数为\((-100)\ +\ 2147483647\ =\ 2147483547\)
那么它们显然满足\((-100)\ ≡\ 2147483547\ mod\ 2147483647\)
\((-100)\)的32位原码是\(1000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0110\ 0100\)
\(2147483547\)的32位原码是\(0111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1001\ 1011\), 刚好是\((-100)\)的原码按位取反. 反码转换规则要求负数保留符号位, 所以没法说这是\((-100)\)的反码, 不过补上符号位1之后即是补码\(1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1001\ 1011 = (-101)\), 这是因为补码中为了使0这个值有唯一表示而把原码中的负0定义为了补码中的\((-1)\)
所以需要加上1去补齐这一对应关系——如此我们便得到了\((-100)\)的补码表示
所以说一个数\(y\)的反码\(x\), 实际上是这个数\(y\)对于同一个模\(m\)的同余数的原码. 而这个模即是这个32位值所能表示的最大值\(2147483647\)
这即是什么在负整数的原码转换成补码时, 保留最高位上的符号位1然后其他位取反在加1就可以得到补码了——这个计算方式的本质就是找这个负数的同余数, 再加1补上被负0占用的位置——所以这种溢出般的跳变其实完全无法避免的, 只能试着去补全它, 因为其本质其实是进位
其实是我移码哒!
这时候我们可以回头看看书本上的说法：所有编码系统的设计, 都在追求连续性和唯一性. 原码, 反码和补码的演化, 就在不断提高整数编码的这两方面性能.
的确如此
因为原码的机制有两个突出的问题使得计算很麻烦,
第一个是它有两种0的表示方式, 第二是它有两个间断点(可以说这两个间断点就是因为0的原因产生的), 以32bit原码为例就是\(0111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ 2147483467\)跳变到\(1000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ =\ (-0)\),以及\(1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ (-2147483467)\)跳变到\(0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ =\ 0\)
于是我们就用反码去修复第二个间断点, 反码中的正数没变化, 最大正数跳变到\(0\)的问题没解决, 不过反码中\(1000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ =\ (-2147483467)\)增加到\(1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ (-0)\)就更加连续, 这样全\(1\)跳变到正\(0\)的问题解决了, 不过\(0111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ 2147483467\)跳变到负\(0\)的问题现在变成了跳变到\(1000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ =\ (-2147483467)\)的问题了
从前文我们能看出, 既然是把全部二进制位直接一分为二用来表示正负整数, 那么这个跳变就不可能被处理掉, 而只可能被移到不同的位置, 所以我们只能做点儿力所能及的事情——处理掉这正负\(0\)的问题
补码就是反码加\(1\), 这个操作就很威: 虽然正整数还是没变化, 但这使得负数补上了一个码, 整体下移了一个单位，曾经的反码最小值\(1000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ =\ (-2147483467)\)被修正到了补码的\(1000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ =\ (-2147483468)\). 这样做的话, 当二进制值继续增加, 真值也会递增, 这符合直觉并且方便于四则运算; 从另一面讲, 补码\(1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ (-1)\)变成了\((-1)\), 继续增大只有一个\(0\). 虽然消除了双\(0\)问题必然有这个结果, 不过这样还将这32位二进制能表示的数增加了一个, 表达范围\(+1\), 实在是一举多得.
不过还是有个问题: 这样来看补码正数从\(0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ =\ 0\)增加到补码的\(0111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ 2147483467\)
单调递增, 但是在二进制值更大的负数部分的时候\(1000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ 0000\ =\ (-2147483468)\)单调递增到\(1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ 1111\ =\ (-1)\). 如果需要快速比较两个二进制值的真值的大小我们需要先确定这两个值的正负性,判断二进制值所在的区间, 然后可能还需要求绝对值来比较数值大小——就很反人类. 所以加上一个偏置值——最大正数, 来把所有数都变成正数
这样就便于一一比较了, 给个表收工吧:
| 补码(二进制) | 补码真值 | 移码真值 | 十六进制 |
|---|---|---|---|
| 0000 0000 0000 0000 0000 0000 0000 0000 | 0 | 2147483467 | 0x 00 00 00 00 |
| 0000 0000 0000 0000 0000 0000 0000 0001 | 1 | 2147483468 | 0x 00 00 00 01 |
| 0000 0000 0000 0000 0000 0000 0000 0010 | 2 | 2147483469 | 0x 00 00 00 02 |
| ...... | ...... | ...... | ...... |
| 0111 1111 1111 1111 1111 1111 1111 1110 | 2147483466 | 4294966933 | 0x 7F FF FF FE |
| 0111 1111 1111 1111 1111 1111 1111 1111 | 2147483467 | 4294966934 | 0x 7F FF FF FF |
| 1000 0000 0000 0000 0000 0000 0000 0000 | -2147483648 | -1 | 0x 80 00 00 00 |
| 1000 0000 0000 0000 0000 0000 0000 0001 | -2147483647 | 0 | 0x 80 00 00 01 |
| 1000 0000 0000 0000 0000 0000 0000 0010 | -2147483646 | 1 | 0x 80 00 00 02 |
| ...... | ...... | ...... | ...... |
| 1111 1111 1111 1111 1111 1111 1111 1110 | -2 | 2147483465 | 0x FF FF FF FE |
| 1111 1111 1111 1111 1111 1111 1111 1111 | -1 | 2147483466 | 0x FF FF FF FF |
跳变保留, 但大小关系竟然统一了, 真是神奇的大自然(全文完)
Published by